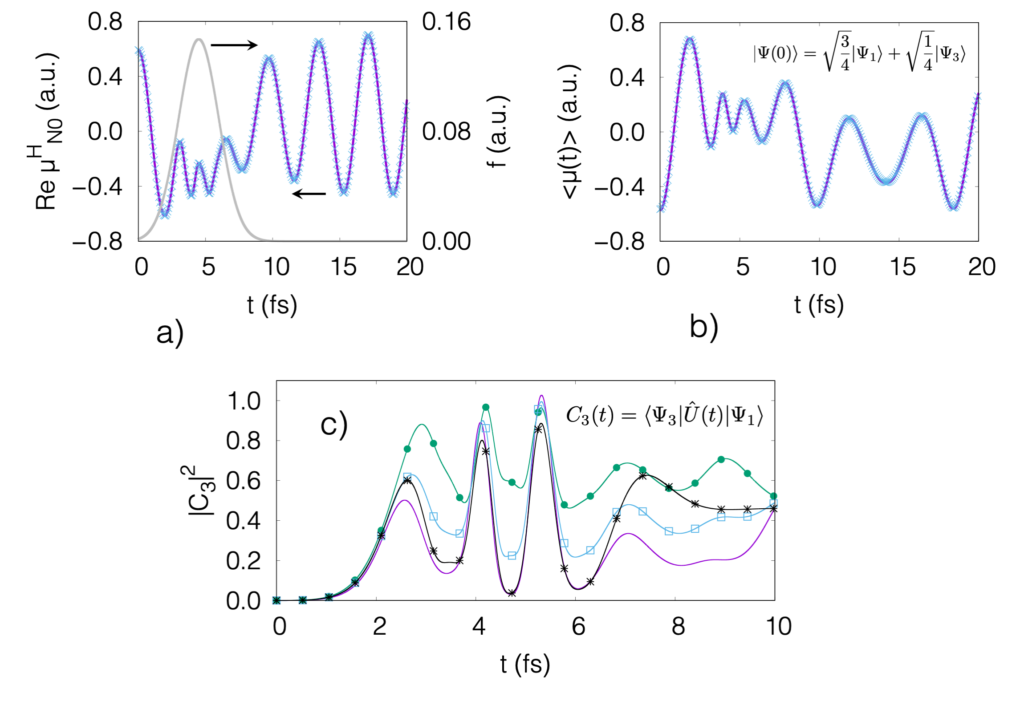
This paper published in Physical Review A shows our theory based on coupled cluster to propagate in principle arbitrary superpositions of quantum states, while maintaining the desired property of size-extensivity. It, size-extensivity, is a fundamental property that physical “large” quantum systems have, and that is difficult to satisfy theoretically speaking. The idea is based on the concept of “second response”: If a system that is initially a linear combination of ground and excited state is propagated, where the “weight” of the excited state is small, by varying such weight one can infer how the excited state would evolve alone (free of the ground state). This idea is somewhat trivial, but when applied to the time-dependent coupled cluster wave function, we obtain a set of equations that describe how the excited state, or a combination of quantum states, changes as a function of time. Link. Update: A follow-up of this work is available at the Electronic Structure journal, Link. This shows a generalization of the formalism and an improved description of populations and coherences.